Applications in Analysis of Ad Hoc Networks using Queuing Theory

Yu Zhang

Abstract

Queuing problems are common scenarios in our daily life. From industrial manufacture to daily queuing, we can never leave this topic. Ad Hoc wireless networks are new kinds of networks. It has the advantages of high flexibility and extensibility, which are applied to our daily life gradually. The paper lists the applications in performance analysis of Ad Hoc networks via using queuing theory, and discusses their pros and cons as well as their development directions. At the end of the article, we reproduce some of the experiments via using MATLAB simulators and give a detailed discussion on the results.

Introduction

Queuing Theory is a model discusses a dynamic service system’s running processes. In this system, the arrival of the customers is an exact stochastic process. When they arrive at the system, they will queue until it’s time for their service. After accepting service, customers are always supposed to leave. For instance, the M/M/1/∞ model (shown in Fig.1) is a classical model used commonly. In this model, we assume the arrival of the customers is an i.i.d. Poisson process and the time interval of only server is an exponential distribution. More importantly, there is an infinite queue length. Many complex models are its variations.

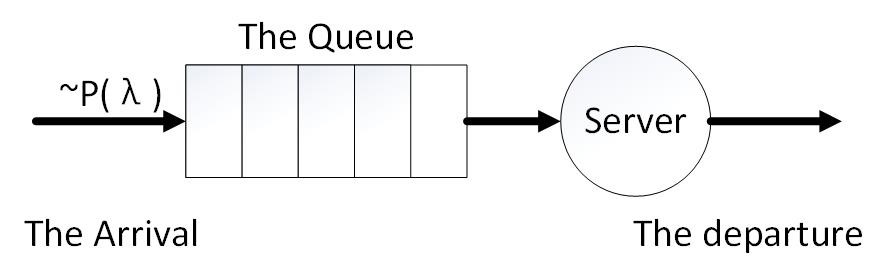
Fig.1 A classical M/M/1 queuing model. In this model, we assume the arrival of the customers is an i.i.d. Poisson process and the time interval of only server is an exponential distribution.

Ad hoc are networks without any base stations, i.e. infrastructure-less. Similar to the ZigBee protocol, they are self-organizing and adaptive networks, who allow spontaneous formation and deformation of networks topology. If node A can connect directly with node B, then they will save the other’s information at their own routing table, respectively. Another scenario is that A can only connect with B via intermedia C (shown in Fig. 2), then all of their routing tables will be updated to ensure that A can sense the existing of B. There are two topologies of ad hoc networks. One is heterogeneous, which means all the nodes have different capabilities. The other is homogeneous, i.e. all nodes have identical capabilities and responsibilities.

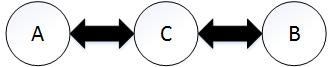
Fig.2 Ad hoc network rules. If A can only connect with B via intermedia C, then all of their routing tables will be updated to ensure that A can sense the existing of B.

There are great number of researches on ad hoc networks, and we can divide them into two kinds. On is to improve the performance via optimizing the protocol, e.g. MACA [1] and MACAW [2]. The former one uses the RTS/CTS mechanism to avoid the hidden terminal problem. And the latter one is an optimization of the first one who can solve the problem of exposed terminal. The other researches are on the problem of which protocol is the best, i.e. how to evaluate the specific system. And we will discuss this topic latter. The rest of the article is organized as follows. The second part of the article (section two) introduces applications in performance analysis of Ad Hoc networks via using queuing theory. The third part of the article (section three) we reproduce some of the experiments via using MATLAB simulators and give a detailed discussion on the results. Finally (section four) is the conclusions.

Performance Analysis of Mobile Ad Hoc Networks using Queuing Theory

Performance studies of ad hoc networks usually focus on either analytical modelling or simulations. We mainly discuss the evaluations via using Queuing theory. There are various publications on this topic. For instance, Jaehyuk Choi [3] analyzes the blocking probability and the queuing delay in the closed loop queue networks with finite queue length by using simulators. Daniele Miorandi [4] analyzes various performance indicators by of the wireless networks with HTTP traffic load by utilizing queuing models. Mustafa Ozdemir [5] analyzes how to design an efficient ad hoc network by using M/MMGI/1/K model. Saikat Ray [6] evaluates the mean delay and collision rate in ad hoc networks with hidden stations by using queuing simulators.
We mainly discuss the Nabhendra Bisnik’s research on evaluating the ad hoc networks by establishing a G/G/1 network model, which seems to be more practical. The basic topology of the model [7] is shown in Fig. 3. The main idea of this paper is using diffusion approximation [8] to solve the G/G/1 model. The variables mentioned in this paper are shown as follow.

• The visit ratio of node i, denoted by ei, is given by

  e_i= p_0i (n)+ ∑p_ji (n)×e_j (1)

• The resulting arrival rate is termed the effective arrival rate at a station. The effective arrival rate at a node i, denoted by ‚i is given by

  λi= λ(e )× e_i (2)

• The utilization factor of station i, denoted by ρi, is given by

  ρ_i= λ_i ⁄ μ_i (3)

• Then by using the diffusion approximation, the paper get the closed form expressions of the mean delay (Formula 4) and the maximum throughput (Formula 5) of the model.

  D(n) = ρ_i⁄((λ×(1-ρ)) ) (4)

  λ_max= p(n)⁄((1/ξ+L/W+4nA(n) L/W ) ) (5)

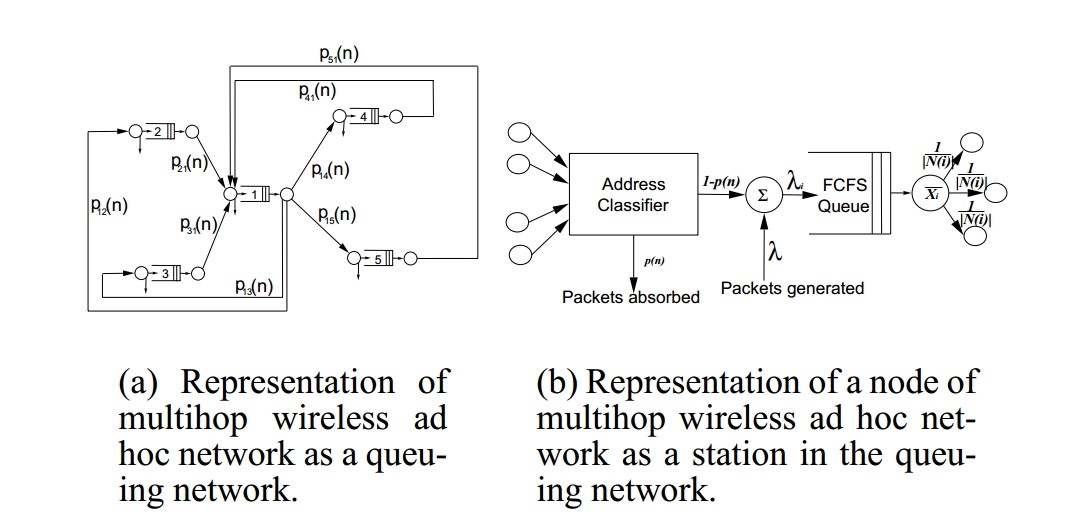
Fig. 3. The G/G/1 model of ad hoc networks with stationary nodes. Figure (a) shows the global nodes where P¬ij(n) means the probability that a package will transfer from node i to node j. While Figure (b) shows a single node in (a), and p(n) means the probability that the destination of a package is this node.

From the above formulas, we can get the knowledge of the interplay of delay (or maximum throughput) and the visit ratio, the utilization factor and so on. However there are also some drawbacks in this research. For example, the mobile nodes are always mobilizable rather than stationary. What’s more, the queue length is always infinite in the real world rather than finite. So there are other researches to optimize this work, e.g. Aznida Hayati Zakaria [9] analyze a practical protocol with finite queue length via using their queue models, more information can refer to the article.

Simulation

For the sake of simplicity, we consider an ad hoc network with only two mobile nods (Fig.4), and more complex scenarios are similar.

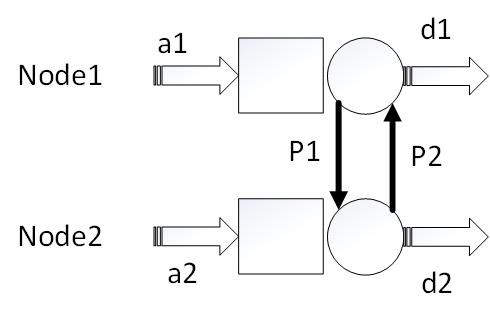
Fig. 4 The simplest ad hoc network model with only two mobile nodes. As we can see in the picture, a1 means the arrival rate of Node1 while d1 is the departure rate, and p1 is the possibility that the page will be delivered to Node2. Node2 is the same.

We can get there are nine states in this model. We express these states in matrix S, whose element S(i,j) means there are i packages in Node1 and j packages in Node2.

s=    (0,0) (0,1) (0,2)
      (1,0) (1,1) (1,2)
      (2,0) (2,1) (2,2)

Easily, we can get the state-transition diagram (Fig. 5).

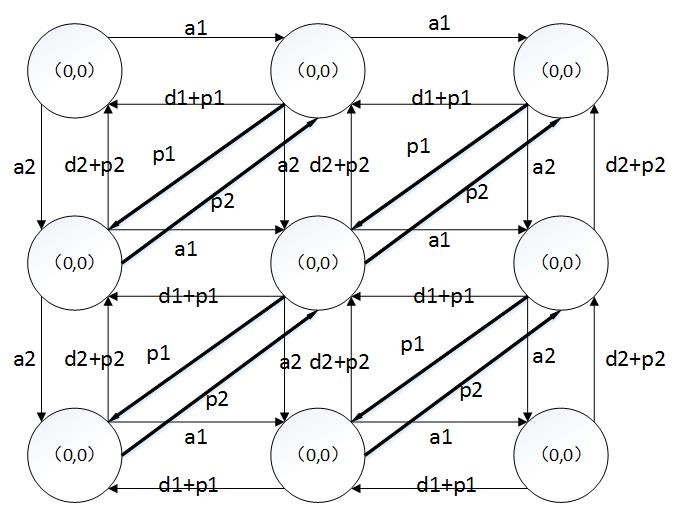
Fig.5 The state-transition diagram. It the basis of our theoretical analysis.

From the above diagram, we can list the balanced equation, and get the stability probabilities of each state.
By using MATLAB, we analysis the package missing rate as well as throughput of each node. In the simulation, we assume that a1=1, a2=10, d1=6, d2=4, p1=2, p2=3, all of which can be got beforehead in real word. Fig.6 and Fig.7 are the simulation results, which denote the relationship between arrival rate (AR) and package missing rate (PMR).

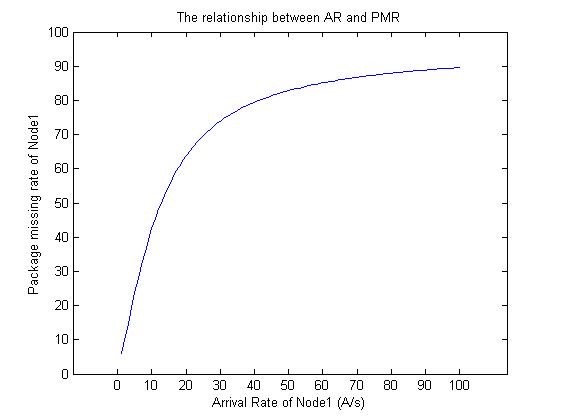
Fig.6 The relationship between arrival rate (AR) of node1 and its own package missing rate (PMR).

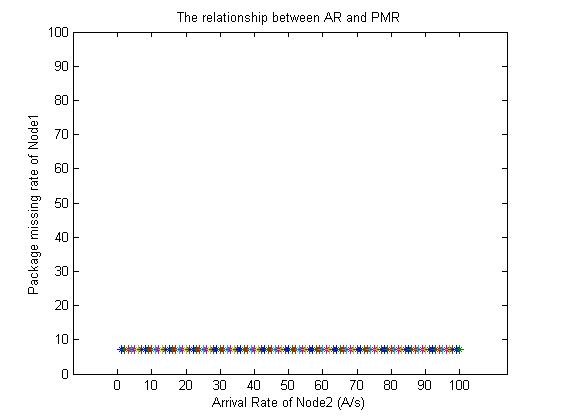
Fig.7 The relationship between arrival rate of node2 and package missing rate of node1.

From the simulation result, we can get that a node’s PMR increases as its own AR increases (Fig.6), while the influence from other nodes’ AR is negligible (Fig. 7). We have also found that a node’s throughput increases until an upper limit as its own AR increases (Fig 8).

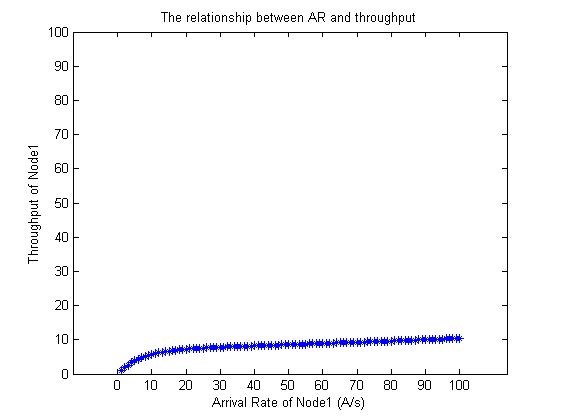
Fig.8 The relationship between AR and throughput.

Conclusions

We first introduce the queuing theory briefly. Then we list the applications in performance analysis of Ad Hoc networks via using queuing theory, and discusses their pros and cons as well as their development directions. Finally we reproduce some of the experiments via using MATLAB simulators and give a detailed discussion on the results, i.e. a node’s PMR increases as its own AR increases, while the influence from other nodes’ AR is negligible. We have also found that a node’s throughput increases until an upper limit as its own AR increases.

Reference

[1] P. Karn. MACA: a new channel access methos for packet radio. In Proceedings of the 9th Comouter Networking Conference, pages 134–140, September 1990.

[2] V. Bharghavan, A. Demers, S. Shenker, and L. Zhang. MACAW: A media access protocol for wireless LANs. In SIGCOMM, pages 212–225. ACM Press, 1994.

[3] G. Zeng, H. Zhu, and I. Chlamtac. A novel queueing model for 802.11 wireless LANs. In Proceedings of WNCG Wireless Networking Symposium, 2003.

[4] D. Miorandi, A. A. Kherani, and E. Altman. A queueing model for HTTP traffic over IEEE 802.11 WLANs. In Proceedings of 16th ITC Specialist Seminar, August 2004.

[5] M. Ozdemir and A. B. McDonald. An M/MMGI/1/K queuing model for IEEE 802.11 ad hoc networks. In Proceedings of PE-WASUN’05, pages 107–111. ACM Press, 2004 .

[6] S. Ray, D. Starobinski, and J. B. Carruthers. Performance of wireless networks with hidden nodes: A queuing-theoretic analysis. To appear in Journal of Computer Communications.

[7] N. Bisnik and A Abouzeid. Queuing Network Models for Delay Analysis of Multihop Wireless Ad Hoc Networks. International Wireless Communications & Mobile Computing Conference, 2006.

[8]G. Bolch, S. Greiner, H. de Meer, and K. S. Trivedi. Queuing Networks and Markov Chains, chapter 10, pages 423–430. John Wiley and Sons, 1998.

[9]A. H. Zakaria, Y. M. Saman, A. S. Noor, etc. Performance Analysis of Mobile Ad Hoc Networks using Queuing Theory. Proceedings of the First International Conference on Advanced Data and Information Engineering, 2013.

Original works, banned reproduced! If use, please indicate the source! ! !

原创作品，禁止转载！若是转载，请注明出处！

赏

嘘寒问暖不如来笔巨款

支付宝

微信